特定年齢人口と自動車保有台数の関係

ガソリン税等が撤廃されたと話題なので、都道府県別自動車保有台数に対して指定の年齢人口との対比を試みることにしました。特定の年齢とは、20歳以上69歳未満の明らかに車両を保有していると考えられる年齢層です。

データの収集

2つのデータを収集します。自動車保有台数と人口に関するデータです。エクセルでダウンロードできます。

都道府県別・車種別保有台数表

自動車検査登録情報協会のサイトからデータをダウンロードします。

参照

読み込み中...読み込み中...

都道府県別年齢別男女人口

都道府県、年齢（5歳階級）、男女別人口－総人口、日本人人口（2024年10月1日現在）のデータをダウンロードします。

参照

読み込み中...読み込み中...

エクセルデータの加工

自動車保有台数の方は綺麗に出力されていますので、とりあえずはこのままにします。

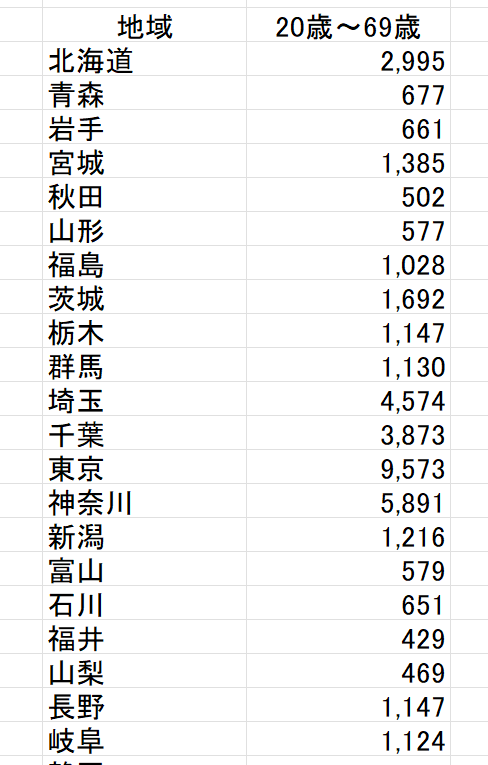
人口の方がひと手間かかりますのでこちらから作業します。ダウンロードしたデータから次のデータ以外削除します。

人口データの加工

1. 人口区分－総人口
2. 性別－男女計
3. 年齢－20歳から69歳まで

下記のようにデータを加工します。

最後は下記のように加工します。

自動車保有台数データの加工

自動車保有台数のデータをベースに加工した人口のデータを対応する都道府県に別に配置できるようにします。ダウンロードしたデータを下記のように加工します。

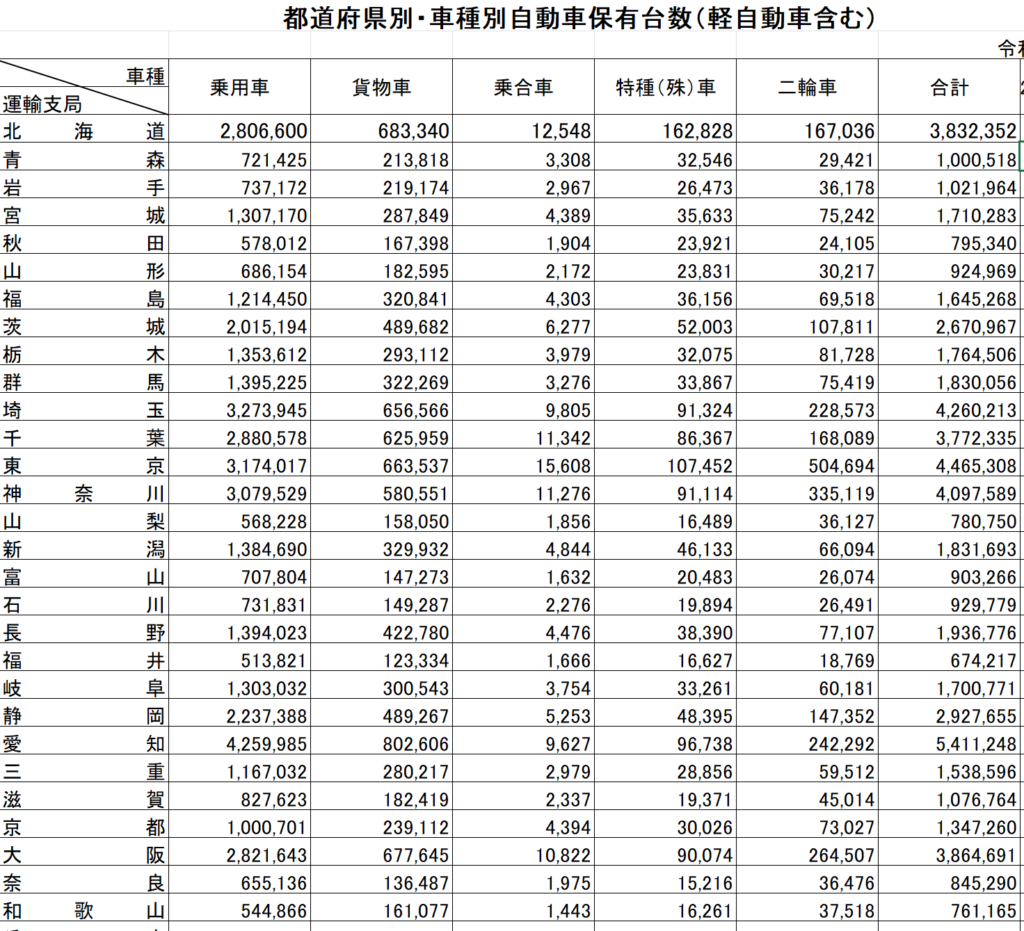
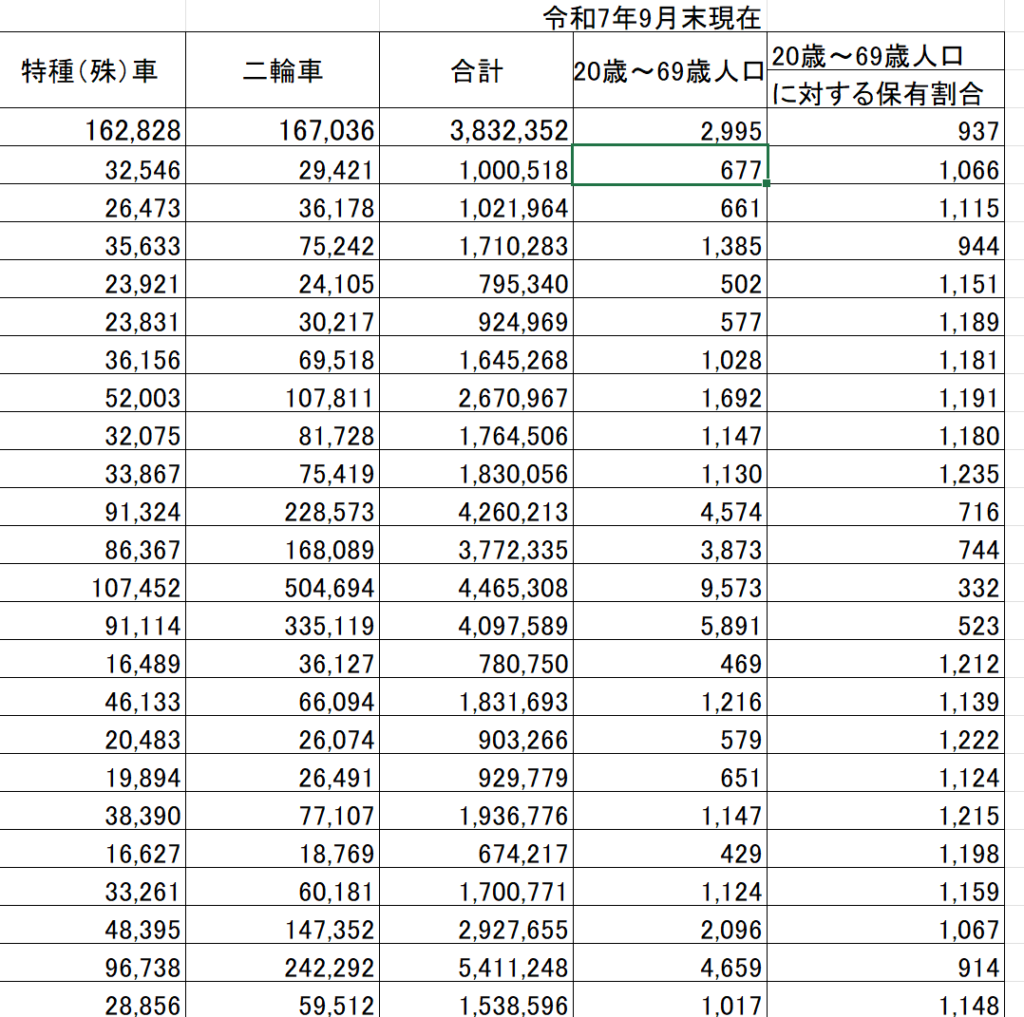
加工が終わったら、下記のように列を追加します。右に20歳から69歳人口とその人口一人当たりの乗用車保有率です。二輪車とか余計なデータはいらないのではと考えるかもしれませんが、案外あとで閃く場合があるので使わなかったとしても残しておきます。

INDEX関数とMATCH関数の使い方

20歳から69歳人口の列に人口データで先程加工したものを貼り付けます。これを関数を使用して行います。INDEX関数とMATCH関数の使い方はWEBで見てもよく分からないと聞きますので、ここで実際のデータを用いて具体的に説明します。

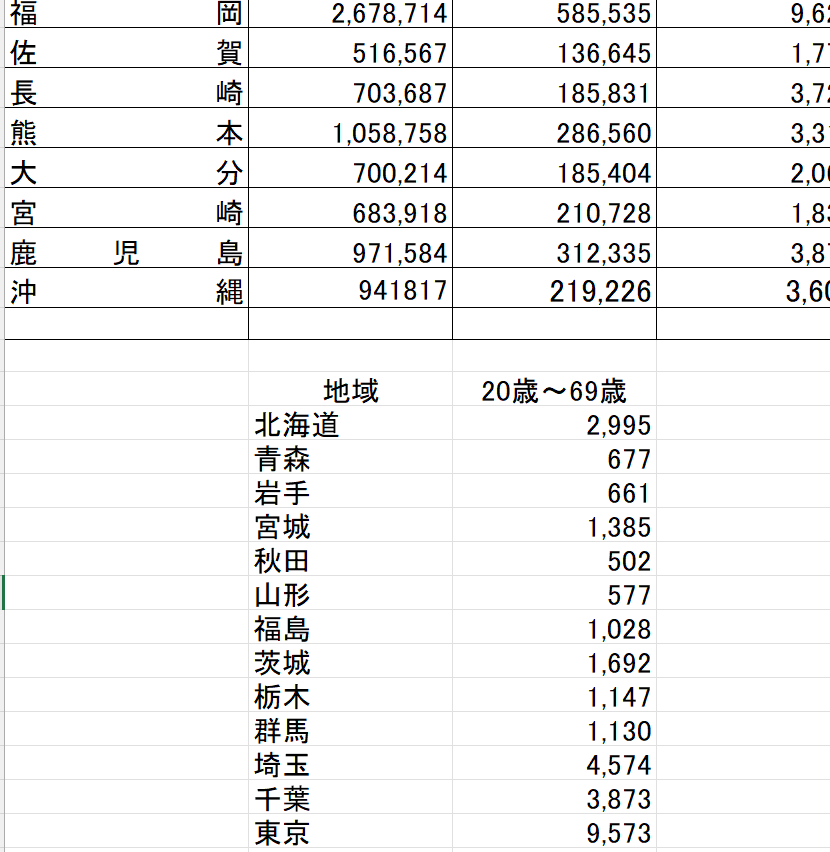
人口データと自動車保有台数のデータを1つのファイルに落とし込みます。B列55行目に北海道、C列55行目数値2,995となるように貼り付けます。

関数を挿入するのは、H列の20歳から69歳人口になります。下記がその関数になります。意味が分からないと思いますので詳しく説明します。下記のコードが今回使用する関数になります。

=INDEX($C$55:$C$101,MATCH(TRIM(A5),TRIM($B$55:$B$101),0))

行の番号と列の番号が交錯する値を返すという関数です。

1. 返したい値の列を指定とは、C列55行目以降にある人口データになります。
2. 行の番号とは、A5の都道府県と合致するB列55行目以降の都道府県のデータがある行番号です。
3. 列の番号とは、合致したB列にある行の番号に対応するC列の番号になります。今回ここは省略しています。なぜなら行の番号に対応する列データがC列だけだからです。D列にもデータがある場合は指定しないといけません。

1. 都道府県名を特定とは、A5以下の都道府県名になります。
2. 検索したい都道府県のある列を指定とは、B55からB101にある都道府県名です。
3. A5とB55以下のデータが完全一致するものだけ値を返すという意味で、0を入力します。

このMATCH関数によって、検索範囲の都道府県が何行目にあるのか数値を返すという意味です。

エクセル関数の一工夫

検索範囲を特定させたうえ、変動しないようにするため$で囲っております。

TRIM関数を使っているのは、各種ダウンロードデータには、全角の空白も含まれていたりする場合もあるので、それをセルごとに除外しておかないと正しくエクセルは認識しません。

• Facebook
• X(旧:Twitter)
• LINE